Premier arpentage

Distances :
• Forme et dimension de la Terre
• Premier arpentage
• Distance Terre-Lune

Une ingénieuse idée...

ARISTARQUE de SAMOS (310 - 230 av. J.-C.), en proposant - avec 17 siècles d'avance sur Nicolas COPERNIC (1473 - 1543) ! - un système héliocentrique, tente une première estimation des distances relatives de la Lune et du Soleil à la Terre.
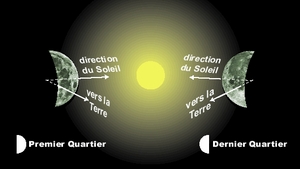
La Lune au Premier Quartier ou au Dernier Quartier montre, vue depuis la Terre, la moitié de sa face éclairée et la moitié de sa face non-éclairée *. Dans ces deux cas, l'axe Soleil-Lune est donc dans une direction perpendiculaire à celui de Terre-Lune.
Il présume que la Lune tourne autour de la Terre à vitesse constante sur une orbite circulaire.
De même, il suppose que le Soleil étant à une distance « finie », les positions de la Lune au Premier Quartier et Dernier Quartier ne sont pas diamétralement opposées.

... pour un résultat tout relatif

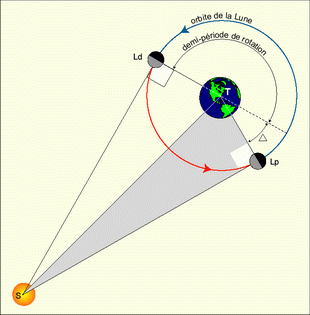
L'écart entre la demi-période de rotation et le temps mis par la Lune pour passer d'un Premier Quartier (Lp) au Dernier Quartier (Ld) permet d'évaluer l'angle Δ (on suppose le mouvement de la Lune parfaitement circulaire et uniforme).
Par une démonstration géométrique simple, on en déduit la distance Soleil-Terre (S-T) en fonction du rayon de l'orbite lunaire T-Lp dans le triangle rectangle T-Lp-S.
Le Soleil étant très éloigné, l'angle Δ est très petit et reste bien inférieur à la précision avec laquelle on détermine l'instant exact d'un Premier Quartier et Dernier Quartier.
à partir de cette méthode, et malgré toute son ingéniosité, ARISTARQUE ne parvint à déduire que le Soleil était entre 18 et 20 fois plus éloigné que la Lune. Il avait trouvé un angle Δ égal à 12 h, alors qu'il n'est que de 35 mn.
C'est pourtant cette valeur, erronée d'un facteur 20 (dans la réalité TS est égal à 400 fois le rayon de l'orbite lunaire), qui sera acceptée durant les 1 500 années suivantes.

* à ne pas confondre avec la face cachée qui est le côté en permanence opposé à la Terre !