Distance Terre-Lune

Distances :
• Forme et dimension de la Terre
• Premier arpentage
• Distance Terre-Lune

Les anciens : rapport Lune/Terre et géométrie

ARISTARQUE (310 - 230 av. J.-C.) émet l'hypothèse que l'ombre de la Terre pouvait être considérée comme un cylindre jusqu'à la distance de l'orbite de la Lune. Lors d'une éclipse centrale *, la Lune reste environ 2 heures dans la zone d'ombre. Se déplaçant d'une distance égale à son diamètre apparent en 1 heure, il calcule que le diamètre lunaire vaut 1/3 de celui de la Terre.

1 - la Lune entre dans l'ombre de la Terre ;
2 - une heure s'est écoulée, la Lune est entièrement éclipsée ;
3 - une première heure dans l'ombre et la Lune s'est déplacée d'un diamètre ;
4 - après deux heures d'éclipse, la Lune sort de l'ombre.

Avec une mauvaise estimation du diamètre de la Lune, la détermination de la distance Terre-Lune est également faussée.

Hipparque, avec une meilleure dimension du cône d'ombre estima cette distance à 38 fois le diamètre de la Terre.

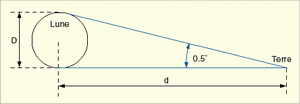
En réalité, l'ombre de la Terre forme un cône d'angle 0.5°, ce qui donne un diamètre lunaire égal à 0.27 fois celui de la Terre. La distance Terre-Lune devient alors égale à 30 diamètres terrestres.
ARISTARQUE semble également avoir par la suite réévalué son diamètre lunaire.
Fixant la période de révolution de la Lune à 29 jours, son déplacement horaire (donc son diamètre) correspond à 360÷(29×24), soit ± 0.5°.
La distance d de la Lune vaut alors : D/tg 0.5°.

Les modernes : parallaxe et radar

En 1751, une expérience menée depuis Berlin en B par Joseph Jérôme LEFRANÇOIS de LALANDE (1732 - 1807) et le cap de Bonne Espérance ** en C par Nicolas Louis de la Lacaille permet de déterminer cette distance par la méthode des parallaxes.
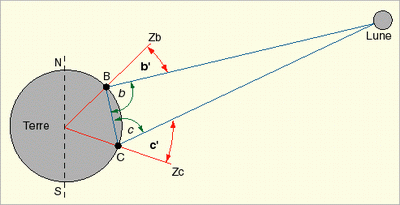
Ils mesurent chacun l'angle séparant leur zénith (Zb et Zc) au centre du disque lunaire lors d'un passage au méridien (soit b' et c'). La distance BC étant connue, il est possible de calculer les angles b et c.
La distance Terre-Lune est déterminée par résolution du triangle B-Lune-C.

Aujourd'hui, à l'aide de signaux radar, il est possible de connaître cette distance avec une grande précision : quelques centimètres ! L'orbite de la Lune étant une ellipse, la distance est de 356 400 km au périgée et portée à 406 700 km à l'apogée, pour une distance moyenne de 384 401 km.

* à ce moment la Lune se trouve sur le plan de l'écliptique et, passant par le centre de l'ombre de la Terre, la durée de l'éclipse est maximale.
** ces deux lieux sont pratiquement sur un même méridien.