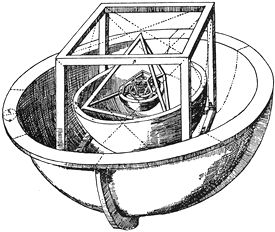
Le modèle planétaire publié par KEPLER dans son Mysterium cosmographicum.

Manquant cruellement de données pour améliorer l'approximation de son modèle, les tensions religieuses prenant des proportions alarmantes à Graz, KEPLER décide de rejoindre Prague où il sait que l'empereur Rodolphe II vient de recueillir Tycho BRAHE. La rencontre avec le célèbre astronome, réputé pour ses observations d'une précision inégalée, a lieu le 4 février 1600. Entre le fougueux KEPLER et le tyrannique BRAHE, les conflits sont incessants. L'hostilité entre les deux hommes s'amenuise cependant peu à peu pour faire place à une réelle collaboration quotidienne. Tycho le charge d'établir la forme exacte de l'orbite de Mars, cette planète présentant un mouvement rétrograde important dont les irrégularités échappent à toute explication. KEPLER pense résoudre l'énigme en quelques jours, il lui faudra six années pour en élucider le mystère.
Suite à une énième beuverie, Tycho meurt le 24 octobre 1601 des suites d'une rétention urinaire ; avant son décès, il désigne KEPLER comme son digne successeur. La requête est acceptée par l'empereur Rodolphe II, le famélique Johannes KEPLER devient Mathématicien impérial, poste qu'il occupera jusqu'à la mort de son souverain en 1612.
En 1609, KEPLER édite le résultat de ses derniers travaux dans Astronomia nova (Astronomie nouvelle), il y énonce ses deux premières lois : l'orbite de chaque planète est une ellipse dont le Soleil occupe l'un des foyers ; le rayon vecteur reliant le Soleil à une planète balaie des aires égales en des périodes égales. Guidé par une recherche de l'harmonie, il publie, en 1619, Harmonice mundi (Harmonie du monde) dans lequel il énonce sa troisième loi : le rapport entre le cube du demi-grand axe de l'orbite et le carré de la période de révolution est constant pour toutes les planètes.
Afin de réduire l'incertitude des mesures, KEPLER étudie également les phénomènes liés à la réfraction atmosphérique et aborde également la physiologie de l'œil. Il rassemble les connaissances de l'époque dans Ad Vitellionem paralipomena **** qui paraît en 1604, un deuxième ouvrage d'optique suivra en 1611 : Dioptrica. Une œuvre posthume sera également publiée : Somnium, seu opus posthumum de astronomia lunari. Ce récit fantastique d'un voyage sur la Lune se veut bien plus qu'un simple récit de (science)-fiction : diffuser les idées coperniciennes en argumentant le mouvement de la Terre *****.
Le 15 novembre 1630, accablé par de nombreuses turpitudes familiales et la maladie, Johannes KEPLER meurt, dans le plus grand dénuement, à Regensburg lors d'un voyage. Deux ans plus tard, sa tombe sera détruite lors de la guerre de Trente Ans. Un cratère lunaire de 32 km (08.1 °N - 38.0 °O) porte son nom, un autre sur Mars ainsi que l'astéroÏde n° 1134.

* - Né prématurément (un 27 décembre, le jour de la saint Johannes), il a de plus failli être emporté par la variole à l'âge de quatre ans. Cette grave maladie lui laissera de terribles séquelles, notamment une très forte myopie.
** - Ce tempérament semble être un héritage familial. Entre son père, Heinrich KEPLER, un mercenaire débauché à la solde du premier fauteur de trouble et sa mère, Katharina GULDENMANN, continuellement enivrée de « plantes médicinales » par une tante qui finira sur le bûcher, la jeunesse de Johannes KEPLER est loin d'être des plus heureuses.
*** - Les polyèdres réguliers (chacune des faces est constituée par un même polygone) sont : cube (6 carrés), tétraèdre (4 triangles), dodécaèdre (12 pentagones), icosaèdre (20 triangles), octaèdre (8 triangles). Chacun de ces polyèdres peut être inscrit dans une sphère et circonscrit à une autre sphère de même centre ; chacun des cercles représente les distances relatives des orbites planétaires. Euclide aurait vécu autour de 300 av. J.-C., il est également possible que ce nom désigne un collectif derrière lequel se seraient cachés plusieurs mathématiciens « à la manière de » Nicolas Bourbaki.
**** - Le titre complet est : Ad Vitellionem paralipomena, quibus astronomiæ pars optica traditur. L'ouvrage est plus connu sous le nom simplifié de Optica.
***** - En 1593, étudiant à l'université de Tübingen, il choisit pour sujet de thèse la manière dont les mouvements célestes peuvent être perçus depuis la Lune. Le sujet est refusé mais l'idée demeure, une première version circule vers 1611 et vaudra quelques désagréments à son auteur. Son gendre et assistant, Jacob BARTSCH (dit Bartsius ou Bartschius, 1600 - 1633), meurt de la peste alors qu'il tente de republier le texte largement enrichi de notes. C'est son fils Ludwig KEPLER qui achèvera la publication en 1634.

* - Entre 1943 et 1949, Kenneth EDGEWORTH, un écrivain et astronome amateur irlandais, avait déjà formulé la même proposition. Pour cette raison, la « Ceinture de Kuiper » se retrouve parfois également dénommée « Ceinture de Edgeworth-Kuiper ».
** - Sedna, Quaoar, ..., sont des objets de la « Ceinture de Kuiper ». Notre planète naine Pluton est de plus en plus soupçonnée d'appartenir à cette classe d'objets ; elle n'en serait que l'un des plus gros et plus proche représentant.